
Madison, WI 53705, U.S.A.
Phone: (608) 238-2171, Fax: (608) 238-9241
Email: info@powline.com
| Home | Search | News | Products |

|
610 N. Whitney Way, Suite 160
Madison, WI 53705, U.S.A. Phone: (608) 238-2171, Fax: (608) 238-9241 Email: info@powline.com |
|||
|
Power Line Systems once again advances the state of the art by providing a simple way to account for structure flexibility and its effects on loads.
Most sag-tension & loads programs operate under the assumption that the wire system is independent from the structure system and that there is no coupling between wires. They neglect the fact that structure deflections impact loads. More importantly, they ignore how a load on one wire can propagate through a flexible structure and affect the tensions in the other wires.
The good news is that structure flexibility can work to your advantage. In unbalanced loading scenarios, structures will often deflect so as to relieve the load. In broken conductor scenarios structure flexibility allows a structure to receive support from the remaining wires rather than taking the full longitudinal imbalance itself.
This page shows several different methods for modeling structure flexibility. We start with a make believe model that clearly illustrates the differences between these methods. We conclude with a real broken conductor situation demonstrating how flexibility analysis greatly reduces the loads on the structure.
The images shown on this page are from our PLS-CADD line design program assisted by plug-in modules SAPS for finite element sag-tension and PLS-POLE for pole/frame analysis.
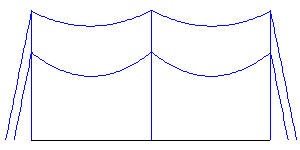
Now we add an extreme ice load to the lower wire in the second span.
As a sanity check we superpose the shape our structure would assume when subjected to these loads (right most figure). A correct analysis requires the structure and wire systems to be in equilibrium. This clearly isn't the case as our structure geometry does not coincide with the wire system geometry.
Later on we will compare the loads and mid span clearances of this method with other more accurate methods.
| Structure usage in percent | 410 |
| Center structure longitudinal load at upper attachment (lbs) | 0 |
| Center structure longitudinal load at lower attachment (lbs) | 18557 |
| Clearance to ground under iced span (ft) | 29.27 |

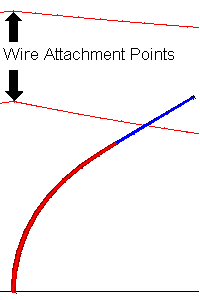
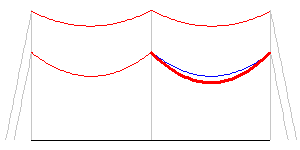
A comparison of our structure and wire geometry reveals we are doing much better than with fixed attachments but that we still have a problem. Our problem arises from the fact that in real life the lower attachment can't move without causing a movement in the upper attachment.
| Structure usage in percent | 33.2 |
| Center structure longitudinal load at upper attachment (lbs) | 0 |
| Center structure longitudinal load at lower attachment (lbs) | 1075 |
| Clearance to ground under iced span (ft) | 24.24 |
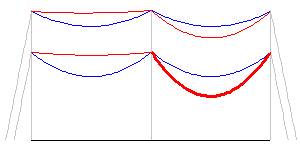
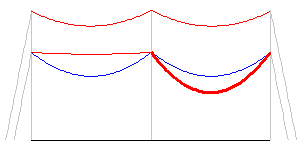
Running the analysis in this fashion reveals the addition of ice has a profound effect on all spans.
The deflected structure view is now very close to the sag-tension geometry shown. The match isn't perfect because the equations we use to relate the displacements of the attachments is a linear approximation.
| Structure usage in percent | 70.3 |
| Center structure longitudinal load at upper attachment (lbs) | 1885 |
| Center structure longitudinal load at lower attachment (lbs) | 4648 |
| Clearance to ground under iced span (ft) | 22.43 |

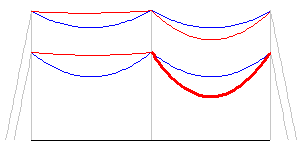
| Structure usage in percent | 69.6 |
| Center structure longitudinal load at upper attachment (lbs) | 1862 |
| Center structure longitudinal load at lower attachment (lbs) | 4368 |
| Clearance to ground under iced span (ft) | 22.19 |
| Pre-Ice | Post-Ice Fixed Attachments L2 |
Post-Ice Spring Constants 600 lbs/ft L2 |
Post-Ice Flexibility Matrix L3 |
Post-Ice Full Structure Models L4 |
|
|---|---|---|---|---|---|
| Structure usage in percent | 0.2 | 410 | 33.2 | 70.3 | 69.6 |
| Longitudinal load at upper attachment (lbs) | 0 | 0 | 0 | 1885 | 1862 |
| Longitudinal load at lower attachment (lbs) | 0 | 18557 | 1075 | 4648 | 4368 |
| Clearance to ground under iced span (ft) | 32.16 | 29.27 | 24.24 | 22.43 | 22.19 |
| Upper attachment longitudinal displacement (ft) | 0.00 | 0.00 | 0.00 | 1.05 | 1.16 |
| Lower attachment longitudinal displacement (ft) | 0.00 | 0.00 | 1.80 | 1.96 | 2.01 |
The use of Full Structure Models is the most accurate of the methods. Unfortunately the time and memory required by this analysis is often prohibitive except in special cases where it is essential to capture nonlinear structure behavior. It is not unusual for a sag-tension run for a single load case to take up to a minute for real lines with complicated frames and towers.
The Flexibility Matrix method provides results that are very close to that of the Full Structure Model method but is much faster. This is generally the recommend method as it provides a reasonable approximation for structure flexibility and the way a structure transfers load between attachments.
The Spring Constant method is not recommended as it fails to account for any coupling between movement at the various attachment points. To get useful results from this method requires that you have sensible values for the spring constant for each attachment point of every structure. For our simplified example this method overestimates the sag by nearly two feet and greatly underestimates the longitudinal load and the structure usage. Despite its many problems this method is frequently used in other programs because it is far easier to implement than more rigorous approaches.
Using Fixed Attachments is the simplest of the available methods and also by far the fastest. It can provide reasonable results under normal loading conditions but it should not be used in cases where unbalanced loads and highly flexible structures can result in measurable structure deflections. In our test case with large tension imbalances and deflections it is unable to produce a meaningful result. Broken conductor scenarios are another case where this method should generally be avoided.
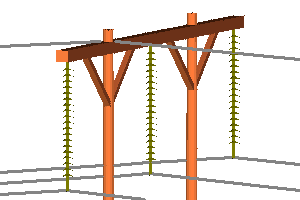
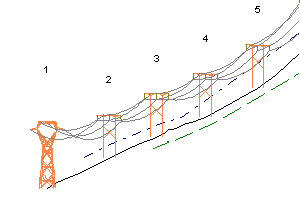
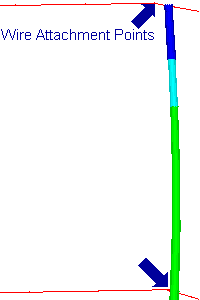
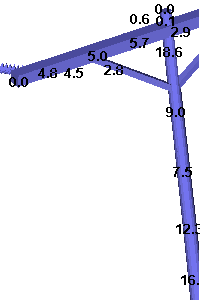
Now we subject a wood H-frame line to a broken conductor to demonstrate how different approaches to sag-tension and structure flexibility impact structure performance. A section of this line is pictured to the right. We will be breaking the ahead span of the left most phase.
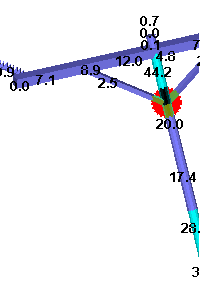
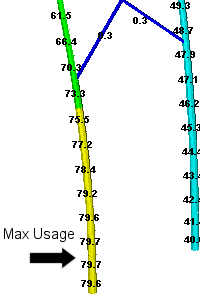
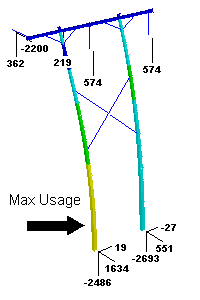
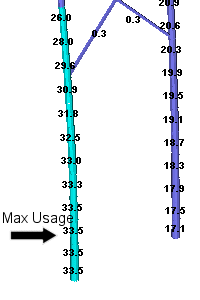
The first picture gives an overview of the entire structure and shows the loads applied to the structure as well as the foundation reactions. The other two pictures show the structure usage near the ground and near the top of the structure.
In this case we have a 2200 lb. longitudinal load at the broken wire attachment point resulting in a structure that at 79.7% of its available capacity near the ground line.
If you are using a ruling span based sag-tension program to compute your loads these are the kinds of results you would get.
Now we run the same analysis again except we account for the reduction in tension that occurs when the suspension insulator swings into the ahead span.
Accounting for the insulator swing reduces the longitudinal load from 2200 lbs. to only 923 lbs. with a similar reduction in the foundation reactions. This structure is still controlled by the left pole slightly above the ground line but its usage has dropped to only 33.5% of capacity.
The suspension insulator has an amazing ability to reduce load imbalances. If you want to take full advantage of its abilities you need a multi-span sag-tension program that is capable of predicting its performance.

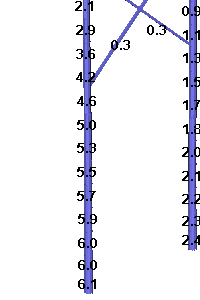
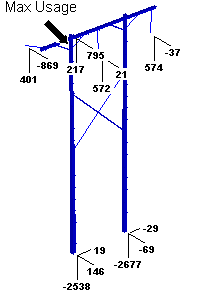
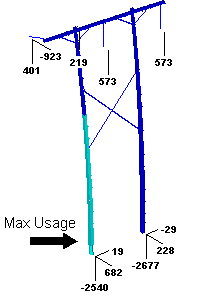
We once again run our analysis except this time we increase the reality level through the use a flexibility matrix to account for structure flexibility and coupling between the different attachments.
We see some pretty drastic changes from the previous analysis that completely ignored the structure behavior. First, at the left most attachment, we see a slight decrease in the longitudinal load (923 lbs. to 869 lbs.). The carrier wire attached at the top of the left structure had its longitudinal load increase from 0 lbs. to 795 lbs. This transfer of load to the carrier wire results in a major reduction in the foundation reactions and in the pole usage while at the same time putting the carrier wire and hardware at risk. The pole usage has dropped from 33.5% to only 10.6% and the critical point on the pole is now near the top rather than at the ground line.
This example shows how crucial it is to consider the impact a structure has on the wire system when working with flexible structures and unbalanced loads. If you fail to consider the structure you do not see the way load gets transferred from the broken attachment to the carrier wire and you would be led to believe your structure strength is limited near the ground line when it is in fact limited near the top of the pole.
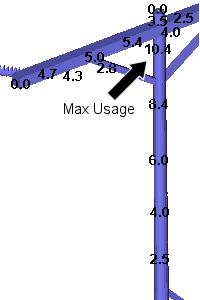
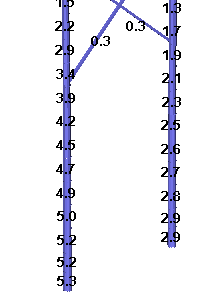
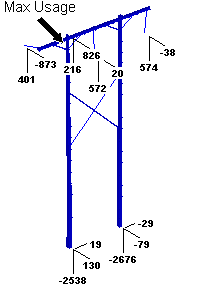
The interesting thing to note about this analysis is just how closely it matches the results we obtained using the flexibility matrix. The loads match to within 30 lbs. This serves as evidence that the flexibility matrix is capturing the fundamental behavior of the structure.
Hopefully the examples above have convinced you that there are situations where structure flexibility can have a major impact on line performance. If you are concerned about structure flexibility, then you need the Power Line Systems suite of programs including PLS-CADD, PLS-POLE, TOWER and SAPS. Our line design suite is the only commercially available tool sophisticated enough to do sag-tension while accounting for structure behavior.
Back to finite element sag-tension technical notes.